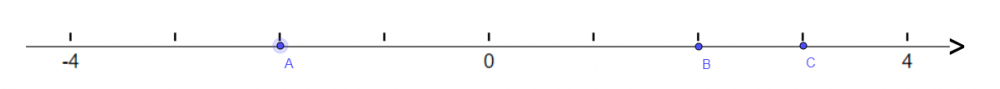Wiskunde 1ste graad A
Getallenleer - de Basis (proeftraject)
Getallenleer - de Basis (proeftraject)
Lestraject bekijken?
Probeer WeZooz Academy meteen even GRATIS uit en start met leren dankzij onze diverse lestrajecten voor vakken in de 1ste graad A!
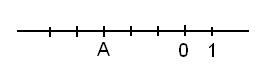
In dit lestraject leer je de basis van de gehele en natuurlijke getallen. Bekijk de video's, maak de oefeningen en los de toets op. Krijg dit onderwerp volledig onder de knie!
Dit
Gratis!
lestraject bestaat uit 8 lessen,
Geschatte duurtijd: 12 minuten.